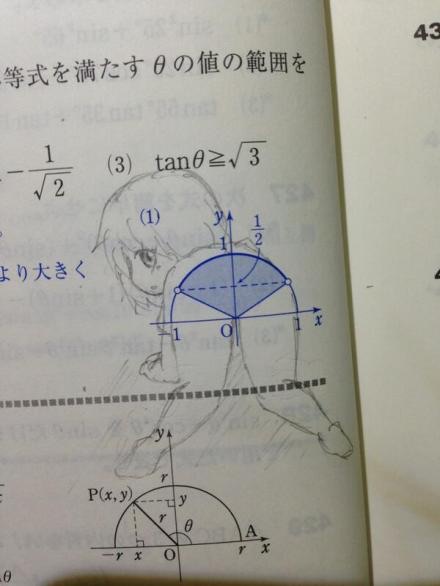
Ubiquitous math


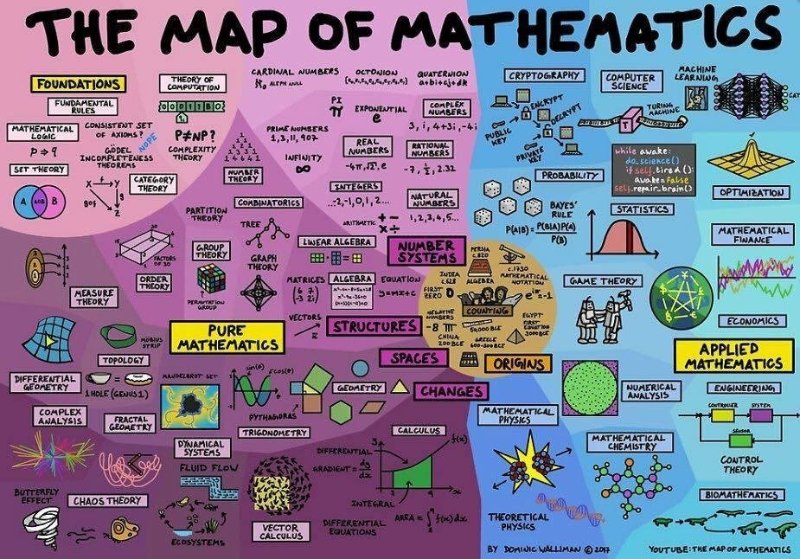 (Map by Dominic Walliman)
(Map by Dominic Walliman)
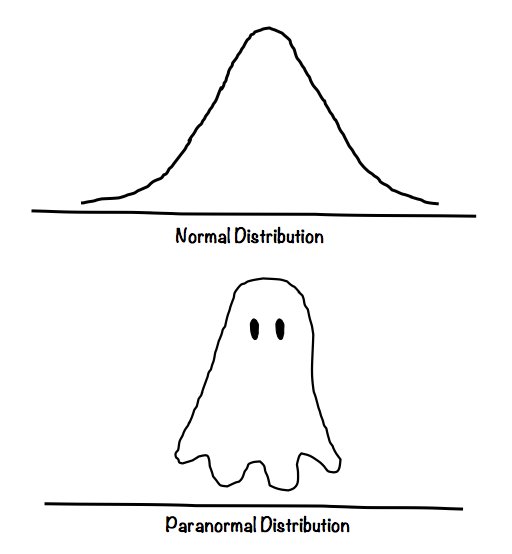

 (source)
(source)

 (source)
(source)
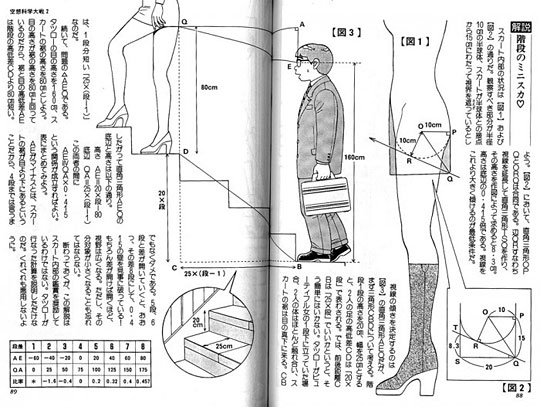 (source)
(source)